Imagine This: The Cosmos
Let’s start by imagining we’re astronauts on a space mission, traveling through the vast expanse of the universe. To navigate, we need to understand where we are, how fast we’re moving, and in what direction. That’s where vectors come into play. Vectors are like the coordinates in our space mission, telling us how to move in this cosmic journey!
What is a Vector?
In the simplest sense, a vector is a quantity that has both a magnitude (how much) and a direction (which way). You can think of it as an arrow pointing from one place to another.
- The magnitude is how long the arrow is (like the distance traveled or speed).
- The direction tells us which way the arrow is pointing (like the direction of travel).
Example 1: Moving Across the Sky
Let’s say you’re in a spaceship, and you’re traveling 10,000 kilometers north. Your vector would be represented as:
- Magnitude = 10,000 km
- Direction = North
If you change direction and travel 10,000 kilometers east instead, you now have a new vector:
- Magnitude = 10,000 km
- Direction = East
But how do we combine these two movements in space?
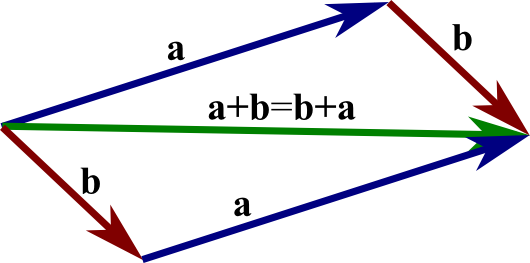
The Power of Adding Vectors
Imagine two arrows in space—one points north, and another points east. These two arrows represent different vectors. To combine them, we use vector addition, which is essentially like drawing the second vector starting from the tip of the first.
Example 2: Vector Addition in Space
You first move 10,000 km north, then 10,000 km east. To find the total displacement (the final position), you connect the start and end of both arrows, forming a right triangle. The result is a new vector—the diagonal line from the start point to the end point.
This diagonal vector’s magnitude is found using the Pythagorean theorem:
Magnitude=(10,0002+10,0002)≈14,142 km
This gives us the resultant vector—the direct path that connects where you started to where you ended up.
Scalars vs Vectors
You might be wondering, how does this relate to scalars? Scalars are quantities that only have magnitude and no direction. Think of temperature or mass. If you say, “The temperature is 25°C,” you don’t need a direction, just the amount. Vectors are different—they tell you not just how much, but which way.
Using Vectors in Real Life
Just like how Sergio Sacani explains the cosmos, vectors are everywhere around us! Take GPS navigation, for instance. When your phone tells you to go 3 miles west and 4 miles north, it’s using vector principles to guide you. The direction of travel and distance form vectors, and your phone is essentially performing vector addition to plot the shortest path to your destination.
Breaking Down the Components: Vector Components
Now, let’s take a deeper look at how we break down vectors. In space, you’re not always going to just travel north or east. Often, you’ll have diagonal directions. This is where we decompose vectors into components.
A vector can be split into two components:
- X-component (horizontal, east/west)
- Y-component (vertical, north/south)
Example 3: Decomposing a Vector
Let’s say your vector points northeast with a magnitude of 10,000 km at a 45° angle. To find the components, you use trigonometry (just like how we calculate angles in the cosmos when we observe stars!).
The X-component (eastward) would be:
X=10,000×cos(45∘)≈7,071 km
The Y-component (northward) would be:
Y=10,000×sin(45∘)≈7,071 km
Now you can move in any direction in space by combining these components!
Final Thoughts: The Universe is Full of Vectors!
Just like Sergio Sacani dives deep into the workings of the universe, vectors help us understand the forces and motions in our world—whether it’s satellites orbiting planets, rockets launching to space, or even the simplest walk across a park. They guide us through the vast unknown and give us the tools to make sense of where we’re headed.
Homework for the Explorer
- Try drawing your own vector diagram! Take two vectors with different directions and add them using the tip-to-tail method.
- Break a vector into components (use different angles, such as 30°, 60°, etc.).
- Look around you—identify things moving in vectors, like the direction the wind is blowing or a car turning on a road!
This is just the beginning of your space journey with vectors! The cosmos is full of them—get ready to explore more!
Extra Information:
Picture This: The Cosmic Right Triangle
Imagine you’re in space again, and you’ve traveled along a diagonal direction—say, 10,000 kilometers at a 45° angle. This direction can be visualized as the hypotenuse of a right triangle, and we want to break that down into two parts: one part moving horizontally (along the x-axis) and the other moving vertically (along the y-axis).
This creates a right triangle where:
- The hypotenuse is the vector you’re dealing with (the 10,000 km at a 45° angle).
- The x-side is the horizontal displacement (moving eastward).
- The y-side is the vertical displacement (moving northward).
Why Cosine for the x-component?
The angle (45°) is formed between the hypotenuse (the vector) and the x-axis (the horizontal direction). To calculate how much of the vector is moving in the x-direction, we need to know how much of the hypotenuse is aligned with that x-axis.
Here’s where cosine comes in. The cosine of an angle gives us the ratio of the adjacent side (the x-component) to the hypotenuse (the vector):
cos(θ)=adjacent/hypotenuse
So, to find the length of the x-component (the horizontal displacement), we multiply the magnitude of the vector by cos(θ):
X-component=Magnitude×cos(θ)
In this case:
X=10,000×cos(45∘)≈7,071 km
This tells you how far you’ve traveled in the horizontal direction (east-west) from your starting point.
Why Sine for the y-component?
The sine function deals with the opposite side of the triangle—the part that’s aligned with the y-axis (the vertical direction). The sine of the angle gives us the ratio of the opposite side (the y-component) to the hypotenuse (the vector):
sin(θ)=opposite/hypotenuse
So, to find the length of the y-component (the vertical displacement), we multiply the magnitude of the vector by sin(θ):
Y-component=Magnitude×sin(θ)
In this case:
Y=10,000×sin(45∘)≈7,071 km
This gives you how far you’ve traveled in the vertical direction (north-south).
Visualizing it
If we visualize the triangle, you can think of the cosine as describing how much of the vector is pointing along the x-axis (the horizontal direction), and the sine as describing how much of the vector is pointing along the y-axis (the vertical direction).
- Cosine gives you the “horizontal” part of the journey (along the x-axis).
- Sine gives you the “vertical” part of the journey (along the y-axis).
Trigonometric Relationship: The Pythagorean Theorem
You can also think of these components in terms of the Pythagorean theorem. The components (x and y) form the two legs of a right triangle, and the vector (hypotenuse) is the diagonal:
Magnitude^2=X-component^2+Y-component^2
Using cosine and sine, we can ensure the components fit together perfectly to make the total magnitude.
Summary
So, the reason we use cosine for the x-component and sine for the y-component is because:
- Cosine tells us how much of the vector points horizontally, relative to the angle.
- Sine tells us how much of the vector points vertically, relative to the angle.
It’s like breaking down a path you’re traveling along into how much of it is going straight forward (cosine) and how much of it is going upward (sine). Both are essential for understanding the complete motion in space!
Keep Exploring!
Once you understand this, you can tackle even more complex situations, like vectors in 3D space or when multiple forces are acting on an object! Keep thinking of the universe in vectors, and you’ll be well on your way to mastering this cosmic journey!
Image: